Question

Stress at work: In a poll conducted by the General Social Survey, 81% of respondents said that their jobs were sometimes or always stressful. One hundred and seventy-five workers are chosen at random. Use the TI-84 Plus calculator as needed. Round your answer to at least four decimal places. (a) Approximate the probability that 150 or fewer workers find their jobs stressful. (b) Approximate the probability that more than 140 workers find their jobs stressful. (c) Approximate the probability that the number of workers who find their jobs stressful is between 146 and 150 inclusive.

Answer 1

We are given that 81% of respondents said that their jobs were sometimes or always stressful.

So, p = 0.81

(a) Approximate the probability that 150 or fewer workers find their jobs stressful.

x = 150

p = 0.81

n = 175

So,
`(x)/(n) =\widehat{p}`

`(150)/(175) =\widehat{p}`

`0.8571=\widehat{p}`

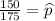
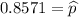
Formula :
`z=\frac{\widehat{p}-p}{\sqrt{(p(1-p))/(n)}}`

`z=\frac{0.8571-0.81}{\sqrt{(0.81(1-0.81))/(175)}}`

`z=1.5882`

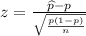
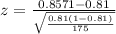
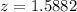
Refer the z table

So, P(z<150)=0.9429

So, the probability that 150 or fewer workers find their jobs stressful is 0.9429

b) Approximate the probability that more than 140 workers find their jobs stressful.

x = 140

p = 0.81

n = 175

So,
`(x)/(n) =\widehat{p}`

`(140)/(175) =\widehat{p}`

`0.8=\widehat{p}`

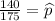
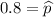
Formula :
`z=\frac{\widehat{p}-p}{\sqrt{(p(1-p))/(n)}}`

`z=\frac{0.8-0.81}{\sqrt{(0.81(1-0.81))/(175)}}`

`z=-0.3372`

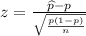
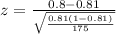
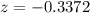
P(z<140) = 0.3707

P(z>140)=1-P(z<140)=1-0.3707=0.6293

So, the probability that more than 140 workers find their jobs stressful is 0.6293

c) Approximate the probability that the number of workers who find their jobs stressful is between 146 and 150 inclusive.

x = 146

p = 0.81

n = 175

So,
`(x)/(n) =\widehat{p}`

`(146)/(175) =\widehat{p}`

`0.8342=\widehat{p}`

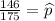
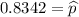
Formula :
`z=\frac{\widehat{p}-p}{\sqrt{(p(1-p))/(n)}}`

`z=\frac{0.8342-0.81}{\sqrt{(0.81(1-0.81))/(175)}}`

`z=0.816`

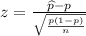
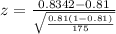
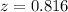
From part a) P(z<150)=0.9429

So,P(z<150)-P(z<146)=0.9429 - 0.8342=0.1087

Hence the probability that the number of workers who find their jobs stressful is between 146 and 150 inclusive is 0.1087