Question

An automobile traveling at a rate of 30 ft/sec is approaching an intersection. When the automobile is 120 ft from the intersection, a truck traveling at the rate of 40 ft/sec crosses the intersection. The automobile and the truck are on roads that are at right angles to each other. How fast are the automobile and the truck seperating 2 sec after the truck leaves the intersection?

Answer 1

14ft/sec

Explanation:

GIVEN: An automobile traveling at a rate of 30 ft/sec is approaching an intersection. When the automobile is 120 ft from the intersection, a truck traveling at the rate of 40 ft/sec crosses the intersection.

IN SKETCH BELOW............. IN THE ATTACHMENT

A IS AUTOMOBILE AND V IS TRUCK AT TIME T= 0

TRUCK IS AT M AFTER T SECONDS...AUTOMOBILE IS AT L AFTER T SECS.

AT=120 '

After T seconds

AL= 30T

LV= 120-30T

VM= 40T

LM =
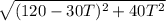`√((120-30T)^2+40T^2)` ( let this be s)

now , ds/dt =
`\sqrt{(2(-30)(120-30T)+3200T)/(2√((120-30T)^2+1600T^2) ) }`

`(ds)/(dt) = (2500T-3600)/(√((120-30T)^2+1600T^2) )`

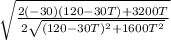
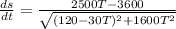
now in this equation put T=2 we get

`(5000-3600)/(√(3600+6400) )`

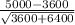
ds/dt= 1400/100= 14 FPS

hence the two vehicles are separating at 14 ft/sec at T=2 seconds