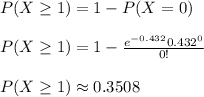Question

The number of failures of a testing instrument from contamination particles on the product is a Poisson random variable with a mean of 0.018 failures per hour. (a) What is the probability that the instrument does not fail in an 8-hour shift? (b) What is the probability of at least 1 failure in a 24-hour day? Round your answers to four decimal places (e.g. 98.7654).

Answer 1

The probability that the instrument does not fail in an 8-hour shift is
`P(X=0) \approx 0.8659`

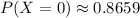
The probability of at least 1 failure in a 24-hour day is
`P(X\geq 1 )\approx 0.3508`

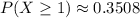
Explanation:

The probability distribution of a Poisson random variable X representing the number of successes occurring in a given time interval or a specified region of space is given by the formula:

`P(X)=(e^(-\mu)\mu^x)/(x!)`

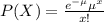
Let X be the number of failures of a testing instrument.

We know that the mean
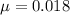`\mu = 0.018` failures per hour.

(a) To find the probability that the instrument does not fail in an 8-hour shift, you need to:

For an 8-hour shift, the mean is
`\mu=8\cdot 0.018=0.144`

`P(X=0)=(e^(-0.144)0.144^0)/(0!)\\\\P(X=0) \approx 0.8659`

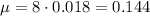
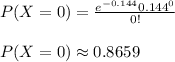
(b) To find the probability of at least 1 failure in a 24-hour day, you need to:

For a 24-hour day, the mean is
`\mu=24\cdot 0.018=0.432`

`P(X\geq 1 )=1-P(X=0)\\\\P(X\geq 1 )=1-(e^(-0.432)0.432^0)/(0!)\\\\P(X\geq 1 )\approx 0.3508`