Question

Suppose the quantity demanded weekly of the Super Titan radial tires is related to its unit price by the equation

p + x2 = 324

where p is measured in dollars and x is measured in units of a thousand. How fast is the quantity demanded weekly changing when

x = 6,

p = 288,

and the price per tire is increasing at the rate of $2/week? (Round your answer to the nearest tire.)

Answer 1

The rate of change of weekly demand is -1/6.

Explanation:

It is given that the quantity demanded weekly of the Super Titan radial tires is related to its unit price by the equation

`p+x^2=324`

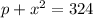
where p is measured in dollars and x is measured in units of a thousand.

We need to find the rate of change in weekly demand, when x=6, p=288 and
`(dp)/(dt)=2`.

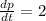Subtract p from both sides.

`x^2=324-p`

Differential with respect to t.

`(d)/(dt)x^2=(d)/(dt)(324-p)`

`2x(dx)/(dt)=-(dP)/(dt)`

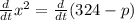
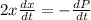
Divide both sides by 2x.

`(dx)/(dt)=-((dP)/(dt))/(2x)`

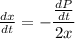
Substitute x=6 and
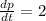`(dp)/(dt)=2` in the above equation.

`(dx)/(dt)=-(2)/(2(6))`

`(dx)/(dt)=-(1)/(6)`

`(dx)/(dt)=-0.16667`

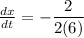
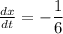
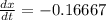
Rate of change in weekly demand is 0 (approximate to the nearest tire). It dose not make any sense.

Therefore, the rate of change of weekly demand is -1/6.