Question

A 1.0 kg copper rod rests on two horizontal rails 1.0 m apart and carries a current of 50 A from one rail to the other.

The coefficient of static friction between rod and rails is 0.60.What are the
(a) magnitude
(b) angle (relative to the vertical) of the smallest magnetic field that puts the rod on the verge of sliding?

Answer 1

given,

mass of copper rod = 1 kg

horizontal rails = 1 m

Current (I) = 50 A

coefficient of static friction = 0.6

magnetic force acting on a current carrying wire is

F = B i L

Rod is not necessarily vertical

`F_x =i L B_d`

`F_y= i L B_w`

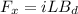
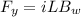
the normal reaction N = mg-F y

static friction f = μ_s (mg-F y )

horizontal acceleration is zero

`F_x-f = 0`

`iLBd = \mu_s(mg-F_y )`

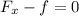
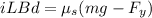
B_w = B sinθ

B_d = B cosθ

iLB cosθ= μ_s (mg- iLB sinθ)

`B = (\mu_smg)/(i(cos\theta +\mu_s sin\theta))`

`\theta =tan{-1}{\mu_s}`

`\theta =tan{-1}{0.6}`

`\theta = 31^0`

`B = (0.6* 1 * 9.8)/(50(cos31^0 +0.6 sin31^0))`

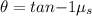
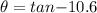
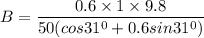
B = 0.1 T