Question

A particular balloon can be stretched to a maximum surface area of 1257 cm2. The balloon is filled with 3.1 L of helium gas at a pressure of 754 torr and a temperature of 294 K . The balloon is then allowed to rise in the atmosphere. Assume an atmospheric temperature of 273 K and determine at what pressure the balloon will burst. (Assume the balloon to be in the shape of a sphere)

Answer 1

The ballon will brust at

Pmax = 518 Torr ≈ 0.687 Atm

Step-by-step explanation:

Hello!

To solve this problem we are going to use the ideal gass law

PV = nRT

Where n (number of moles) and R are constants (in the present case)

Therefore, we can relate to thermodynamic states with their respective pressure, volume and temperature.

`(P_1V_1)/(T_1)=(P_2V_2)/(T_2)` --- (*)

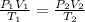Our initial state is:

P1 = 754 torr

V1 = 3.1 L

T1 = 294 K

If we consider the final state at which the ballon will explode, then:

P2 = Pmax

V2 = Vmax

T2 = 273 K

We also know that the maximum surface area is: 1257 cm^2

If we consider a spherical ballon, we can obtain the maximum radius:

`R_(max) = \sqrt{(A_(max))/(4 \pi)}`

Rmax = 10.001 cm

Therefore, the max volume will be:

`V_(max) = (4)/(3) \pi R_(max)^3`

Vmax = 4 190.05 cm^3 = 4.19 L

Now, from (*)

`P_(max) = P_1 (V_1T_2)/(V_2T_1)`

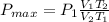
Therefore:

Pmax= P1 * (0.687)

That is:

Pmax = 518 Torr