Question

The average starting salary for this year's graduates at a large Texan university is $45,000, with a standard deviation of $4,000. Furthermore, it is known that the starting salaries re normally distributed. What is the probability that a randomly selected graduate will have a starting salary of $50,000? Please determine the Z value.

Answer 1

The probability that a randomly selected graduate will have a starting salary of $50,000 or more is 10.56%

Step-by-step explanation:

The formula for calculating a z-score is:

Z=
`(x-μ)/(σ)`

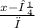
Where:

x=Score in this case is $50,000

μ=Mean or average of the salary: $45,000

σ= standard deviation of $4,000.

Z=
`(50000-45000)/(4000)`

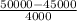
Z= 1.25

This value has an associated probability of 0.8944= 89.44%, this means 89.44% of graduates will have a starting salary of $50,000 or less.

But if we want to know the probability that the graduate has a salary of $50,000 or more, taking into account a population of 100%=1

1-0.8944= 0.1056

Which represents that 10.56% of population of graduates will earn $50,000 or more.