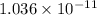Question

The parallel plates in a capacitor, with a plate area of 5.40 cm2 and an air-filled separation of 4.30 mm, are charged by a 4.60 V battery. They are then disconnected from the battery and pulled apart (without discharge) to a separation of 8.10 mm. Neglecting fringing, find (a) the potential difference between the plates, (b) the initial stored energy, (c) the final stored energy, and (d) the work required to separate the plates.

Answer 1

Step-by-step explanation:

given,

plate area = 5.40 cm²

separation = 4.30 mm

Capacitance =
`(\epsilon A)/(d)`

=
`(8.85* 10^(-12)* 5.4* 10^(-4))/(4.3 * 10^(-3))`

=
`1.11 * 10^(-12) F`

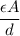
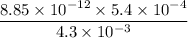
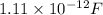
Potential difference applied = 4.6 V

charge stored in the capacitor =
`4.6 * 1.11 * 10^(-12)`

=
`5.106 * 10^(-12)`

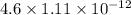
Now when plates are moved new capacitance

Capacitance =
`(\epsilon A)/(d)`

=
`(8.85* 10^(-12)* 5.4* 10^(-4))/(8.10 * 10^(-3))`

=
`0.59 * 10^(-12) F`

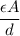
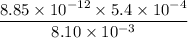
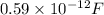
voltage =
`(5.106 * 10^(-12))/(0.59 * 10^(-12))`

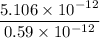
potential applied = 8.65 V

Initial energy stored =
`(1)/(2)C_1V^2`

=
`(1)/(2)* 1.11 * 10^(-12) 4.6^2`

=
`1.174* 10^(-11) J`

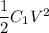
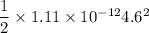
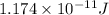
Final energy stored =
`(1)/(2)C_1V^2`

=
`(1)/(2)* 0.59 * 10^(-12) 8.65^2`

=
`2.21* 10^(-11) J`

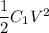
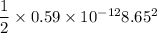
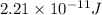
Work done = final energy - initial energy

=
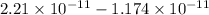
`2.21* 10^(-11) - 1.174* 10^(-11)`

=
`1.036* 10^(-11)`