ANSWER:
An equation has a degree of 2 then the equation is quadratic.
SOLUTION:
Given, an equation has a degree of 2.
We have to find whether an equation which has degree 2 becomes quadratic equation or not.
When we see in detail about quadratic, it is a Latin originated word, describes something pertaining to squares.
We know that, general form a quadratic equation is
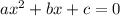
Where a, b, c are constant coefficients of
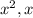 and constant respectively.
and constant respectively.
And, a ≠ 0 is an must to satisfy condition because when a = 0, the term
 becomes zero.
becomes zero.
Which means quadratic equation is any equation having degree 2.
Hence, an equation has a degree of 2 then the equation is quadratic equation.