Answer:

Explanation:
If sketch of the circle and its points is shown as in the accompanying image, notice that the triangle formed FEC is an isosceles triangle, of which we know the angle at the center (angle ECF) to measure
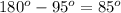 .
.
Since the other two remaining angles must be equal to each other (they are opposite to sides of the same length - radii CE and CF of the circle), we have that the sum of all must render
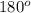 :
:
