Question

If the center thickness of a lens variés more than 0.150 millimeter from the target thickness of 5.000 millimeters, the lens cannot be used. Write and solve an absolute value equation to find the extreme acceptable values for the center thickness of the lens.

Answer 1

All real numbers greater than or equal to 4,999.85 millimeters and less than or equal to 5,000.15 millimeters

Explanation:

Let

x -----> values for the center thickness of the lens

we know that

The absolute value that represent this problem is

`\left|x-5,000\right|\le 0.150`

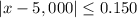
Solve the absolute value

First case (positive)

`+(x-5,000)\le 0.150`

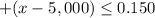
Adds 5,000 both sides

`x\le 0.150+5,000`

`x\le 5,000.15\ mm`

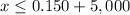
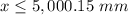
Second case (negative)

`-(x-5,000)\le 0.150`

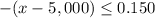
Multiply by -1 both sides

`(x-5,000)\ge -0.150`

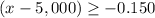
Adds 5,000 both sides

`x\ge -0.150+5,000`

`x\ge 4,999.85\ mm`

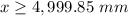
therefore

The extreme acceptable values for the center thickness of the lens is the interval [4,999.85,5,000.15]

All real numbers greater than or equal to 4,999.85 millimeters and less than or equal to 5,000.15 millimeters