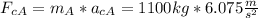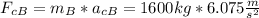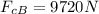Question

Two cars are traveling at the same speed of 27 m/s on a curve thathas a radius of 120 m. Car A has a mass of 1100 kg and car B has amass of 1600 kg. Find the centripetal acceleration and thecentripetal force for each car.

Answer 1

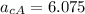`a_(cA) = 6.075` m/s²

`a_(cB) = 6.075` m/s²

`F_(cA) = 6682.5 N`

`F_(cB) = 9720 N`

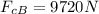
Step-by-step explanation:

Normal or centripetal acceleration measures change in speed direction over time. Its expression is given by:

`a_(c) = (v^(2) )/(r)` Formula 1

Where:

`a_(c)` : Is the normal or centripetal acceleration of the body ( m/s²)

v: It is the magnitude of the tangential velocity of the body at the given point

.(m/s)

r: It is the radius of curvature. (m)

Newton's second law:

∑F = m*a Formula ( 2)

∑F : algebraic sum of the forces in Newton (N)

m : mass in kilograms (kg)

Data

`v_(A) = 27 (m)/(s)`

`v_(B) = 27 (m)/(s)`

`m_(A) = 1100 kg`

`m_(B) = 1600 kg`

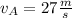
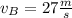
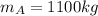
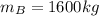
r= 120 m

Problem development

We replace data in formula (1) to calculate centripetal acceleration:

`a_(cA) = ((27)^(2) )/(120)`

`a_(cA) = 6.075` m/s²

`a_(cB) = ((27)^(2) )/(120)`

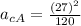
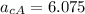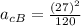
`a_(cB) = 6.075` m/s²

We replace data in formula (2) to calculate centripetal force Fc) :

`F_(cA) = m_(A) *a_(cA) = 1100kg*6.075(m)/(s^(2) )`

`F_(cA) = 6682.5 N`

`F_(cB) = m_(B) *a_(cB) = 1600kg*6.075(m)/(s^(2) )`

`F_(cB) = 9720 N`