Question

A rotating wheel has a constant angular acceleration. It has an angular velocity of 5.0 rad/s at time t=0 s, and 3.0 s later has an angular velocity of 9.0 rad/s. What is the angular displacement of the wheel during the 3.0-s interval?

(a) 15 rad
(b) 21 rad
(c) 27 rad
(d) There is not enough information given to determine the angular displacement.

Answer 1

Angular displacement will be 21 rad

So option (b) will be correct answer

Step-by-step explanation:

We have given initial angular velocity
`\omega _i=5rad/sec`

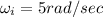
Final angular velocity
`\omega _f=9rad/sec`

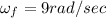
Time t = 3 sec

Angular acceleration is given by
`\alpha =(\omega _f-\omega _i)/(t)=(9-5)/(3)=1.333rad/sec^2`

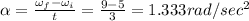
Now angular displacement is given by
`\Theta =\omega _it+(1)/(2)\alpha t^2=5* 3+(1)/(2)* 1.333* 3^2=21rad`

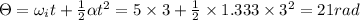
So option (b) will be correct option