Question

There is a goose that lays golden eggs, one each year, arriving at the end of the year. Each egg weighs one pound. The price of gold is currently $1,247 per ounce (16 ounces in a pound), and this is your best guess for the price going forward. You expect the goose to live 10 years (thus laying 10 eggs). The discount rate is 8%. How much is this goose worth today? Assume the goose provides no additional value (e.g., companionship, food) and that expenses are negligible.

a- $41,409
b- $44,227
c- $92,765
d- $101,236
e- $133,880

Answer 1

Option (e) is correct.

Step-by-step explanation:

Each year 1 Golden egg, we get which is weighted at 1 pound

1 pound = 16 ounces

Therefore,

1 golden egg = 16 ounces

= 16 ounces × $1,247 per ounce

= $19,952

Hence, for 10 years discounted at 8% goose shall be:

= Yearly cash flow × Sum of discounting factor (8%) for 10 years

= $19,952 × 6.7101

= $133,880

Note: Discounting factor table is attached with this answer and a discount factor for a specific years is calculated as:

`Discount\ factor=(1)/((1+i)^(t) )`

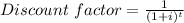
where,

i = interest rate

t = no. of years

Please see the highlighted column in the attachment.