Question

Mr. Shamir employs two part-time typists, Inna and Jim, for his typing needs. Inna charges $15 an hour and can type 6 pages an hour, while Jim charges $18 an hour and can type 8 pages per hour. Each typist must be employed at least 8 hours per week to keep them on the payroll. If Mr. Shamir has at least 208 pages to be typed, how many hours per week should he employ each typist to minimize his typing costs?

Answer 1

The minimum cost would be 480$ when Inna works for 8 hours and Jim works for 20 hours.

Explanation:

We are given the following information in the question:

Charges for 1 hour for Inna = $15

Number of pages typed by Inna in 1 hour = 6

Charges for 1 hour for Jim = $18

Number of pages typed by Jim in 1 hour = 8

Let x be the number of hours Inna work and let y be the number of hours Jim work.

Total cost =
`15x + 18y`

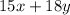
We have to minimize this cost.

Then, we can write the following inequalities:

`6x + 8y \geq 208\\x \geq 8\\y \geq 8\\`

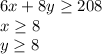
The corner points as evaluated from graph are: (8,20) and (24,8)

C(8,20) = 480$

C(24,8) = 504$

Hence, the minimum cost would be 480$ when Inna works for 8 hours and Jim works for 20 hours.

The attached image shows the graph.