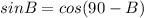Question

Which relationship in the triangle must be true? Triangle A B C is shown. Angle A C B is a right angle. The length of side C B is a, the length of side A C is b, and the length of side A B is c. Sin(B) = sin(A) sin(B) = cos(90 – B) cos(B) = sin(180 – B) cos(B) = cos(A)

Answer 1

b

sin(b)=cos(90-b)

Explanation:

Answer 2

sin(B) = cos(90 – B)

Explanation:

In a right triangle, there are specific trigonometric relations called trigonometric reasons. In any right triangle like it's shown in the image attached, we have:

`sinB=(b)/(c)`

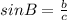
Now, the angle
`90-B` is actually equal to angle
`A`, because angles
`A` and
`B` are complementary, they sum 90°. So, we have:
`90-B=A`.

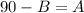Then, from trigonometric reasons we have:

`cosA=(b)/(c)`

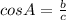
But,
`cosA=cos(90-B)`

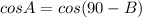
So,

`sinB=(b)/(c)=cosA=cos(90-B)`

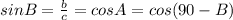
Hence,
`sinB=cos(90-B)`