Question

A researcher wishes to estimate the mean amount of money spent per month on food by households in a certain neighborhood. She desires a margin of error of $30. Past studies suggest that a population standard deviation of $248 is reasonable. Estimate the minimum sample size needed to estimate the population mean with the stated accuracy.A. 274B. 284C. 264D. 272

Answer 1

C. 264

Explanation:

Assuming the random variable for amount of money spent per month on food is normal distributed and the researcher wants to estimate the mean with
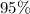`95\%` confidence. Then we can use the following formula to determine the minimum sample size:

`n_0 = \bigg((z_((\alpha)/(2))S_d)/(e) \bigg)^2`

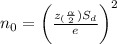
Where
`S_d` is the standard deviation and
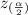`z_{((\alpha)/(2))}` is the quantile of the normal distribution with an area of
`(\alpha)/(2)`.

`n_0 = \big((z_((0.025))*248)/(30) \big)^2 = \big((1.96*248)/(30) \big)^2 \approx 263`

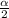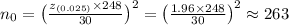
So we need at least 264 households to sample.