Answer: 0.0516
Explanation:
Given : The number of defective components produced by a certain process in one day has a Poisson distribution with a mean of
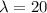 .
.
The probability mass function for Poisson distribution:-
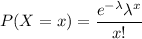
For x= 15 and
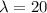 , we have
, we have
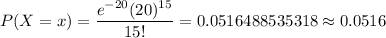
Hence, the probability that exactly 15 defective components are produced in a particular day = 0.0516