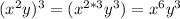Question

Place the indicated product in the proper location on the grid. (3x ^2a - 4y ^a z^3a)^ 2

Answer 1

`9x^(4a) -24x^(2a)y^(a)  z^(3a)  + 16y^(2a) z^(6a)`

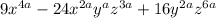
Explanation:

You can follow this steps:

For the expression:

`(3x^(2a) - 4y^(2) z^(3a) )^(2)`

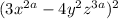
Write the factors:

`(3x^(2a) - 4y^(2) z^(3a) )(3x^(2a) - 4y^(2) z^(3a) )`

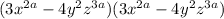
Now multiply by the term
`3x^(2a)`

`(3x^(2a) - 4y^(2) z^(3a) )(3x^(2a) - 4y^(2) z^(3a) ) = 9x^(4a) -12x^(2a) y^(a) z^(3a)`

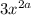
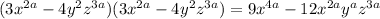
Then multiply by the term
`-4y^(2)`

`(3x^(2a) - 4y^(2) z^(3a) )(3x^(2a) - 4y^(2) z^(3a) ) = 9x^(4a) -12x^(2a) y^(a) z^(3a) \\\\             <strong> -12x^(2a) y^(a) z^(3a) + 16y^(2a) z^(6a)</strong>`

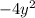
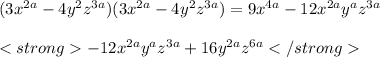
Finally add the terms:

`= 9x^(4a) -24x^(2a) y^(a) z^(3a) + 16y^(2a) z^(6a)`

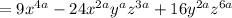
You will need to review the laws for the exponents.

For example:

When you are multiplying with the same base you need to add the exponents.

`x^(2) *x^(5) = x^(2+5) = x^(7)`

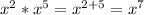
Power to power, you multiply the exponents but keep the same base:

`(x^(2)y)^3 = (x^(2*3) y^3) = x^(6) y^3`