Question

Suppose a basketball player has made 390 out of 434 free throws. If the player makes the next 2 free throws, I will pay you $40.Otherwise you pay me $169

Step 1 of 2: Find the expected value of the proposition. Round your answer to two decimal places. Losses must be expressed as negative values.

Step 2 of 2: If you played this game 588 times how much would you expect to win or lose? Round your answer to two decimal places. Losses must be entered as negative.

Answer 1

Answer: a) -$0.19, b) -$111.72 .

Explanation:

Since we have given that

Number of free throws = 434

Number of throws made by them = 390

Amount for making the next 2 free throws = $40

Amount otherwise he has to pay = $169

a) Find the expected value of the proposition.

Expected value of success in next 2 free throws =
`(390)/(434)* (391)/(435)=0.8077`

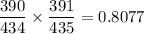
Expected value would be

`0.8077* 40+(1-0.8077)* -169\\\\=32.308-32.4987\\\\=-\$0.19`

b) If you played this game 588 times how much would you expect to win or lose?

Number of times they played the game = 588

So, Expected value would be

`588* -0.19\\\\=-\$111.72`

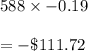
Hence, a) -$0.19, b) -$111.72