Question

Sleep apnea is a disorder in which there are pauses in breathing during sleep. People with this condition must wake up frequently to breathe. In a sample of 427 people aged 65 years and older, 104 of them had sleep apnea. a) Find a Point Estimate for the proportion of people aged 65 years and older who have sleep apnea. Round to 2 decimal places. b) Use your calculator to construct a 99% Confidence Interval. Indicate your basic keystrokes and round your interval to 2 decimal places. c) Interpret your Confidence Interval. In another study, medical researchers concluded that about 15% of elderly people have sleep apnea. Use your confidence interval from part "b" to explain why that does or does not seem

Answer 1

a) 0.24356 or 24.36%

b) [102.39 , 105.61]

c) The interpretation of this confidence interval is that in samples of 427 people aged 65 years and older, there is a 99% probability that the number of people that suffers sleep apnea is between 103 and 105.

Explanation:

a)

This can be considered a binomial distribution (a person either has sleep apnea or not).

Based on the sample we have the probability of suffering the condition is

p = 104/427 = 0.24356

and q (the probability of not suffering the condition) is

q=1-0.24356=0.75644

So the proportion of people aged 65 years and older who have sleep apnea is 0.24356 or 24.36%

b)

To check if we can approximate this binomial distribution with the Normal distribution we must see that

np ≥ 5 and nq ≥ 5

where n is the sample size. Since

427*0.24356 ≥ 5 and 427*0.75644 ≥ 5

we can approximate the binomial with a Normal distribution with mean

np = 427*0.24356 = 104

and standard deviation

`\large s=√(npq)=√(427*0.24356*0.75644)=8.867`

The 99% confidence interval (without the continuity correction factor) is given by the interval

`\large [\bar x-z^*(s)/(\sqrt n), \bar x+z^*(s)/(\sqrt n)]`

where

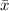`\large \bar x` is the sample mean

s is the sample standard deviation

n is the sample size

`\large z^*` is the 0.01 (99%) upper critical value for

the Normal distribution N(0;1).

The value of
`\large z^*` can be found either by using a table or a computer to find it equals to

`\large z^*=2.576`

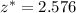
and our 99% confidence interval (without continuity correction) is

`\large [104-2.576*(8.867)/(√(427)), 104+2.576*\frac{8.867}{\sqrt {427}}]=[102.8946,105.1054]`

We can now introduce the continuity correction factor. This should be done because we are approximating a discrete distribution (Binomial) with a continuous one (Normal).

This is simply done by widening the interval in 0.5 at each end, so our final 99% confidence interval is

[102.3946 , 105.6054] = [102.39 , 105.61] rounded to 2 decimal places.

c)

The interpretation of this confidence interval is that in samples of 427 people aged 65 years and older, there is a 99% probability that the number of people that suffers sleep apnea is between 103 and 105.

If another study found a 15% of elderly people suffered sleep apnea, that would mean that in a sample of 427 only 64 would have the condition. Since that number is less than 103 by far, that would give us a reason to doubt about the conditions that framed the study (sample size, sampling method, age of people, etc.)