a. Let
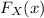 be the CDF of
be the CDF of
 . The CDF of
. The CDF of
 is
is
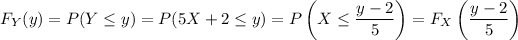
which is to say,
 is also normally distributed, but with different parameters. In particular,
is also normally distributed, but with different parameters. In particular,
![E[Y]=E[5X+2]=5E[X]+2=17](https://img.qammunity.org/2020/formulas/mathematics/college/kh0y9sbio55za08jntymt4sx5v1vwck5vk.png)
![\mathrm{Var}[Y]=\mathrm{Var}[5X+2]=5^2\mathrm{Var}[X]=100](https://img.qammunity.org/2020/formulas/mathematics/college/qkxf46c7219i1b1cr0saslvo5a6y266tc2.png)
b. Using the appropriate CDFs, we have
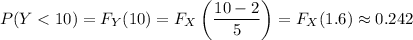
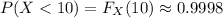
c. The 99th percentile for any distribution
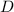 is the value of
is the value of
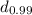 such that
such that
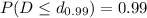 , i.e. all values of
, i.e. all values of
 below
below
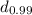 make up the lower 99% of the distribution.
make up the lower 99% of the distribution.
We have
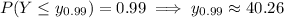
d. On the other hand, the 99th percentile for
 is
is
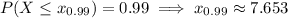
e. We have
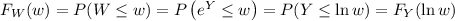
which suggests that
 is normally distributed, or
is normally distributed, or
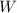 is log-normally distributed. Recall that the moment-generating function for
is log-normally distributed. Recall that the moment-generating function for
 is
is

But we also have
![M_Y(t)=E[e^(tY)]=E[e^(t\ln W)]=E[W^t]](https://img.qammunity.org/2020/formulas/mathematics/college/34wlnjhhiauebmt3rwdb3s5m86qia9bh1o.png)
Then
![E[W]=M_Y(1)=e^(67)](https://img.qammunity.org/2020/formulas/mathematics/college/hz3e9roetlv4n98in8qncfvy3a2i27i6mu.png)
and
![E[W^2]=M_Y(2)=e^(234)\implies\mathrm{Var}[W]=E[W^2]-E[W]^2=e^(234)-e^(134)](https://img.qammunity.org/2020/formulas/mathematics/college/t5q0ezrgn6rnk6dv6x7qxzasxc36q6xx6u.png)