Question

An article presents measures of penetration resistance for a certain fine-grained soil. Fifteen measurements, expressed as a multiple of a standard quantity, had a mean of 2.64 and a standard deviation of 1.06. Find a 95% confidence interval for the mean penetration resistance for this soil. Round the answers to three decimal places.

Answer 1

[2.053 , 3.227]

Explanation:

The 95% confidence interval is given by the interval

`\large [\bar x-t^*(s)/(\sqrt n), \bar x+t^*(s)/(\sqrt n)]`

where

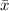`\large \bar x` = the sample mean

s = the sample standard deviation

n = the sample size

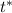`\large t^*` is the 0.05 (5%) upper critical value for the Student's t-distribution with 14 degrees of freedom (sample size -1), which is an approximation to the Normal distribution for small samples (n<30).

Either by using a table or the computer, we find

`\large t^*= 2.145`

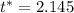
and our 95% confidence interval is

`\large [2.64-2.145*(1.06)/(√(15)), 2.64+2.145*(1.06)/(√(15))]=\boxed{[2.053,3.227]}`