Question

A line with a slope of 3 passes

through the points (2, -1) and (4, 5).
Which of the following is not an
equation of the line that passes
through those points?
B. y = 3x-11
A. y+1 = 3(x-2)
D. y-5 = 3(x-4)
C. y = 3x-7

Answer 1

Answer:b

Explanation:

Answer 2

We conclude that only the equation y = 3x-11 is not an equation of the line that passes through the points.

Hence, option B is correct.

Explanation:

Given the points

• (2, -1)

• (4, 5)

Finding the slope between (2, -1) and (4, 5)

`\mathrm{Slope}=(y_2-y_1)/(x_2-x_1)`

`\left(x_1,\:y_1\right)=\left(2,\:-1\right),\:\left(x_2,\:y_2\right)=\left(4,\:5\right)`

`m=(5-\left(-1\right))/(4-2)`

`m=3`

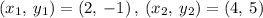
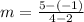
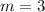
Using the point-slope form of the line equation

`y-y_1=m\left(x-x_1\right)`

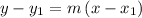
where m is the slope of the line and (x₁, y₁) is the point

substituting the values m = 3 and the point (2, -1)

`y-y_1=m\left(x-x_1\right)`

`y-2=3\left(x-\left(-1\right)\right)`

`y-2=3\left(x+1\right)`

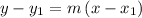
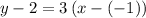
Add 2 to both sides

`y-2+2=3\left(x+1\right)+2`

`y=3x+5`

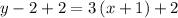
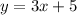
So, y = 3x+5 is one of the equation lines.

We can also check by substituting the values m = 3 and the point (4, 5)

`y-y_1=m\left(x-x_1\right)`

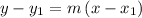
y - 5 = 3(x-4)

So, y - 5 = 3(x-4) is also one of the equation lines.

Now, let say take the point (4, 5) an substitute in y = 3x-11

y = 3x-11

put x = 4 and y = 5

5 = 3(4)-11

5 = 12-11

5 = 1

FALSE!

Hence, the equation y = 3x-11 does not pass through (4, 5). Thus, the equation y = 3x-11 is not an equation of the line that passes through the points.

Now, let say take the point (4, 5) an substitute in y+1 = 3(x-2)

y+1 = 3(x-2)

put x = 4 and y = 5

5+1 = 3(4-2)

6 = 3(2)

6 = 6

TRUE!

Now, let say take the point (2, -1) an substitute in y+1 = 3(x-2)

-1+1 = 3(2-2)

0 = 0

TRUE!

Thus, the equation y+1 = 3(x-2) is an equation of the line that passes through the points.

Now, let say take the point (2, -1) an substitute in y = 3x-7

y = 3x-7

put x = 2 and y = -1

-1 = 3(2) - 7

-1 = 6-7

-1 = -1

TRUE!

Now, let say take the point (4, 5) an substitute in y = 3x-7

y = 3x-7

put x = 4 and y = 5

5 = 3(4)-7

5 = 12-7

5 = 5

TRUE!

Thus, the equation y = 3x-7 is an equation of the line that passes through the points.

Conclusion:

We conclude that only the equation y = 3x-11 is not an equation of the line that passes through the points.

Hence, option B is correct.