Question

As part of a promotion for a new type of cracker, free trial samples are offered to shoppers in a local supermarket. The probability that a shopper will buy a packet of crackers after tasting the free sample is 0.200. Different shoppers can be regarded as independent trials. If X is the number among the next 100 shoppers who buy a packet of the crackers after tasting a free sample, then the probability that fewer than 30 buy a packet after tasting a free sample is ______ .

Answer 1

Answer: Our required probability is 0.99338.

Explanation:

Since we have given that

n = 100

p = 0.200

So,
`np=100* 0.2=20>5`

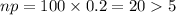
So, we can apply normal approximation.

Mean = 20

Standard deviation =
`√(npq)=√(100* 0.2* 0.8)=√(16)=4=\sigma`

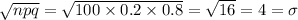
Since
`z=\frac{\bar{X}-\mu}{\sigma}`

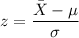
So, Probability that fewer than 30 but a packet after testing a free sample is given by

`P(X<30)\\\\=P(z<(30-20)/(4))\\\\=P(z<(10)/(4))\\\\=P(z<2.5)\\\\=0.9938`

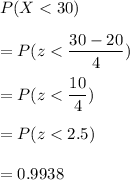
Hence, our required probability is 0.99338.