Question

The curve produced by the water coming from a hose is sketched onto a graph with zeros at 1 and 5. The point (4,

1) also lies on the curve. If h(x) represents the vertical distance from where the water first comes out of the hose and
x represents the horizontal distance, which statements are true? Check all that apply
The scenario can be represented by the function h(x)=-0256)(x-5).
The scenario can be represented by the function h(x)= 16)(x + 5).
The vertex is on the line x=25.
The greatest height that the water reaches is 15 units.
The scenario can be represented by the function h(x)=-166-5).

Answer 1

answer A and C are right

Answer 2

A and C.

Explanation:

From the problem, we deduct that the function has to be quadratic, because it's mention two zeros, which is proper of a polynomial expression with grade 2.

So, we can say that:

`h(x)=a(x-0)(x-5)`

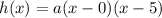
Because, 5 and 0 are roots of the expression.

Also, we know that the point
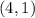`(4,1)` is on the curve, this means:

`h(4)=1`

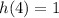
Replacing this relation in the first expression, we have:

`1=a(4-5)`

`1=a(-1)\\a=-1`

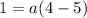
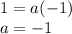
So, the expression would be:

`h(x)=-1(x-0)(x-5)`

`h(x)=-x(x-5)`

`h(x)=-x^(2) +5x`

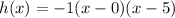
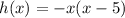
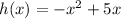
If we graph, we could get the vertex easier.

You can see in the image, that the vertex is at x = 2.5

Therefore, the option C is the answer.

However, the first option has this function:

h(x) = –0.25(x)(x – 5).

Which also can be solution, because, if we try x = 4:

h(4) = –0.25(4)(4 – 5)=1

Therefore, option A is also part of the answer.