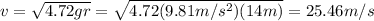Question

The National Aeronautics and Space Administration (NASA) studies the physiological effects of large accelerations on astronauts. Some of these studies use a machine known as a centrifuge. This machine consists of a long arm, to one end of which is attached a chamber in which the astronaut sits. The other end of the arm is connected to an axis about which the arm and chamber can be rotated. The astronaut moves on a circular path, much like a model airplane flying in a circle on a guideline. The chamber is located 14.0 m from the center of the circle. At what speed must the chamber move so that an astronaut is subjected to 4.72 times the acceleration due to gravity? _____________________ m/s

Answer 1

`v=25.46m/s`

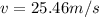
Step-by-step explanation:

The equation for centripetal acceleration of an object that moves in a circle of radius r at velocity v is:

`a_(cp)=(v^2)/(r)`

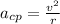
So we can write this velocity as
`v=\sqrt{a_(cp)r}`

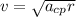
Our chamber is r=14m from the center of the trajectory, and we want our centripetal acceleration to be 4.72g, where g is
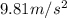`9.81m/s^2`, so with these values we have:

`v=√(4.72gr)=√(4.72(9.81m/s^2)(14m))=25.46m/s`