Question

Barrons reported that the average number of weeks an individual is unemployed is 17.5 week. assume that for the population of all unemployed individuals the population mean length of unemployment is 17.5 weeks and that the population standaard deviation is 4 weeks. Suppose you would like to select a sample of 50 unemployment individuals fo a follow up study.

A) show the sampling distribution of x, the sample mean average for a sample of 50 unemployment individuals.

B) What is the probability that a simple random sample of 50 unemployment individuals will provide a sample mean within one week of the population mean?

C) What is the probability that a simple random sample of 50 unemployed individuals will provide a sample mean within a half week of the population mean?

Answer 1

`\mu = 17.5`

`\sigma = 4`

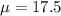
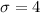
n = 50

A) show the sampling distribution of x, the sample mean average for a sample of 50 unemployment individuals.

We will use central limit theorem

So, mean of sampling distribution =
`\mu_{\bar{x}}=\mu = 17.5`

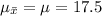
Standard deviation of sampling distribution =
`\sigma_{\bar{x}}=(\sigma)/(√(n))= 0.5656`

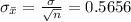
B) What is the probability that a simple random sample of 50 unemployment individuals will provide a sample mean within one week of the population mean?

A sample mean within one week of the population mean means
`x-\mu = 1`

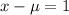
So,
`P(|x-\mu|<1)=P(-1<x-\mu<1)`

=
`P((-1)/((4)/(√(50)))<(x-\mu)/((\sigma)/(√(n))) <(1)/((4)/(√(50))))`

=
`P(-1.77<Z<1.77`

=
`P(z<1.77)-P(z<-1.77)`

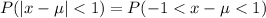
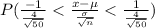
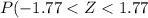
=0.9616-0.0384

=0.9232

The probability that a simple random sample of 50 unemployment individuals will provide a sample mean within one week of the population mean is 0.9232.

C) What is the probability that a simple random sample of 50 unemployed individuals will provide a sample mean within a half week of the population mean?

A sample mean within one week of the population mean means
`x-\mu = 1`

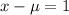
So,
`P(|x-\mu|<0.5)=P(-0.5<x-\mu<0.5)`

=
`P((-1-0.5)/((4)/(√(50)))<(x-\mu)/((\sigma)/(√(n))) <(0.5)/((4)/(√(50))))`

=
`P(-0.88<Z<0.88`

=
`P(z<0.88)-P(z<0.88)`

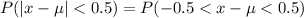
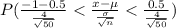
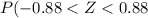
=0.8106-0.1894

=0.6212

The probability that a simple random sample of 50 unemployed individuals will provide a sample mean within a half week of the population mean is 0.6212