Question

Find the distance between points M and N. and if anyone could kinda explain how they got it so i can do the next ones on my own

Answer 1

See photo for steps and the answer is square root of 13

Answer 2

`√(13) = D`

Explanation:

Method #1

We can draw a right triangle on the graph upon where the points are located and use the Pythagorean Theorem:

`{a}^(2) + {b}^(2) = {c}^(2)`

`{3}^(2) + {2}^(2) = {c}^(2)`

`9 + 4 = {c}^(2)`

`13 = {c}^(2)`

`√(13) = c`

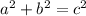
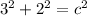
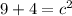
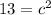
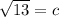
* Whenever we talk about distance, we ONLY want the NON-NEGATIVE root.

_______________________________________________

Method #2

We can use the Distance Formula:

`\sqrt{[-x_1 + x_2]^(2) + [-y_1 + y_2]^(2)} = D`

N[−3, 2] M[−6, 0]

`\sqrt{[3 - 6]^(2) + [0 + 2]^(2)} = D`

`\sqrt{[-3]^(2) + 2^(2)} = D`

`√(9 + 4) = D`

`√(13) = D`

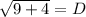
* Whenever we talk about distance, we ONLY want the NON-NEGATIVE root.

** You see? It does not matter which method you choose, as long as you are doing the work correctly.

I am delighted to assist you anytime.