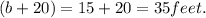Answer:
The dimensions of the rectangular garden: Width = 15 feet and Length = 35 feet.
Solution:
Let the width of the rectangular garden be ‘b’ ft . Then the length of the rectangular garden is ‘b+20’ width.
In the question it is given that the area of the rectangular garden is 525 ft.
We know,
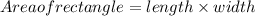
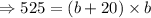
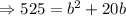
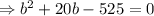
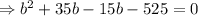
On taking the common terms out we get,
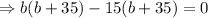
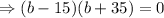
Therefore, Either
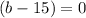 or
or
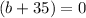
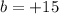 or
or
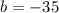
Taking the positive value of b i.e. b= 15 we get width of the rectangular field to be 15 feet and the length of the rectangular garden to be