Question

Two quantities vary inversely. If the value of the first is 15 when the value of the second is 18, find the value of the

second quantity when the first is 10.​

Answer 1

13

Explanation:

When the first quantity is 15, the second quality is 18. This means that the second quality is 3 more than the first quality.

If the first quantity is 10, what is the value of the second quantity?

10 + 3 = 13

Answer 2

27

Explanation:

Let the first quantity be y

Let the second quantity be x

Since the two quantities vary inversely, therefore, the first, y varies inversely to the second, x:

`y\alpha (1)/(x)`

∴
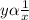
`y = (k)/(x)` .................................. (1)

where k is the constant of proportionality.

When the first, y = 15, the value of the second, x = 18

∴ From eqn (1), we have to find k

`15 = (k)/(18)`

k = 15 x 18 = 270

Now, the value of the second quantity x, when the first y = 10 is

`10 = (270)/(x)`

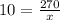
Making x subject of formular, we have

`x= (270)/(10) = 27`

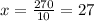
The value of the second quantity is 27