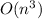Answer:
The proof is in the explanation
Step-by-step explanation:
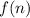 is
is
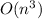 if
if
 for
for
 .
.
So, basically, we have to solve the following inequality

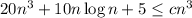
Dividing everything by
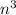 to simplify, we have
to simplify, we have
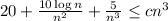
I am going to use
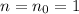 . So
. So


There is a solution for the inequality, which proves that
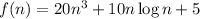 is
is