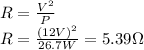Question

The Iceberg Kid, infamous for imposing a deep freeze on whoever disagrees with him, discovers that in his advanced teenaged years his hands constantly feel chilled. As he is a cool physics student, the Iceberg Kid quickly calculates the resistance of the resistor needed to warm his hands. Given that 161 J of thermal energy is generated by the resistor during 6.03 s of operation while connected to a 12.0 V battery, find the correct value of this resistance (and avoid a cold, cold fate).

Answer 1

The resistance is 5.39 Ω

Step-by-step explanation:

We can calculate the resistance of the resistor knowing its power and the voltage across it by:

`P= (V^(2) )/(R) \\\\R=(V^(2) )/(P)`

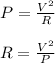
The thermal energy generated by the resistor is equal to the energy dissipated by it. We want to know the power (energy per unit of time) dissipated by the resistor:

`P=(energy)/(time)=(161J)/(6.03 s) =26.7 W`

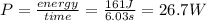
Now that we know what is the power dissipated and the voltage across it (as it is the only element connected to the battery, by Kirchhoff's voltage law, it has to be the same as the one generated by the battery), we find the resistance:

`R=(V^(2) )/(P)\\R=((12V)^(2) )/(26.7W)=5.39 \Omega`