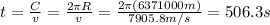Question

A science fiction story I once read had the premise that a small, heavy piece of rock could orbit a planet at a height of 1.5 m. Because of this, the natives would always duck down when walking across the small moon's path, a behavior that seemed inexplicable to the explorers who had recently arrived but who didn't know about the moon. If air resistance weren't a problem, and such a situation existed on earth, (a) how fast would the moon travel and (b) how long would the orbital period be

Answer 1

`v=7905.8m/s`

`t=506.3s`

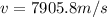
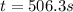
Step-by-step explanation:

The force of gravity between the Earth, of mass
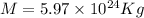`M=5.97*10^(24)Kg` and a rock of mass m orbiting at a distance that would be the radius of the Earth R=6371000m (1.5m is insignificant) would be:

`F=(GMm)/(R^2)`

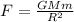
Where
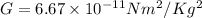`G=6.67*10^(-11)Nm^2/Kg^2` is the gravitational constant.

Under this force, the rock experiments a (centripetal) acceleration given by:

`F=ma=m(v^2)/(R)`

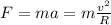
Putting all together:

`m(v^2)/(R)=(GMm)/(R^2)`

`v^2=(GM)/(R)`

`v=\sqrt{(GM)/(R)}`

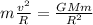
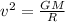
Which for our values is:

`v=\sqrt{((6.67*10^(-11)Nm^2/Kg^2)(5.97*10^(24)Kg))/((6371000m))}=7905.8m/s`

And since the circumference of the orbit would be
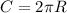`C=2\pi R`, the time taken to travel it would be:

`t=(C)/(v)=(2\pi R)/(v)=(2\pi (6371000m))/(7905.8m/s)=506.3s`