Question

Pure acid is to be added to a 10% acid solution to obtain 90L of 22% solution. What amount of each solution should be used?

Answer 1

Mix the following to obtain the desired solution:

• 
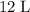  `\rm 12 \; L` of the 100%-pure acid solution, and
• 
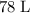  `\rm 78\; L` of the 22% acid solution.

Assumption:

After mixing, the volume of the final solution is equal to the volume of the 22% solution plus the volume of the pure acid solution.

Explanation:

Let the volume of the pure acid required be
`\rm x` liters.

The volume of the final solution is given to be 90 liters. If the assumption is true, the volume of the 22% solution has to be equal to
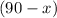`(90 - x)` liters.

`\text{Solvent} = \text{Solution} * \text{Concentration}`.

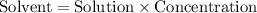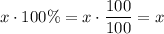Amount of solvent from that
`x` liters pure acid solution:

`\displaystyle x \cdot 100\% = x \cdot (100)/(100) = x`.

Amount of solvent from that
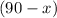`(90 - x)` liters of 10% acid solution:

`\displaystyle (90 - x) \cdot 10\% = (90 -x) \cdot (10)/(100) = 9 - 0.1 x`.

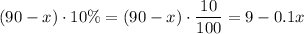Solvent from the two solutions, combined:

`x + (9 - 0.1x) = 0.9x + 9`.

Concentration the mixed solution:

`\displaystyle \text{Concentration} = \frac{\text{Solvent}}{\text{Solution}} = (0.9x + 9)/(90) = 0.01x + 0.1`.

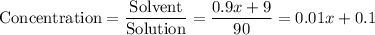This concentration is expected to be equal to

`\displaystyle 22\% = (22)/(100) = 0.22`.

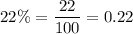In other words,

`0.01x + 0.1 = 0.22`.

Solve for
`x`:

`x = 12`.

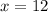That is:
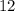`12` liters of the pure acid is required. Another
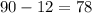`90 - 12 = 78` liters of the 22% solution will be required.