Answer:
P(x >16.5) = 0.3372
Step-by-step explanation:
Given data:
P = 0.07
n = 166
Available vegetarian dinner is 16
let
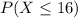 is number of short vegetarian meals
is number of short vegetarian meals
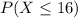 = binomial distribution (166, 0.09)
= binomial distribution (166, 0.09)
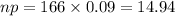
n(1-p) = 166(1-0.09) = 151.06
Both value of np and n(1-p) greater than 5
x - normal distribution with
mean = np = 14.94
standard deviation
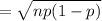
[/tex]= \sqrt{14.94(1-0.09)}[/tex]
standard deviation = 3.687
Find P(x> 16) i.e P(X>16 ) = P(x >16.5)
P(x >16.5) = 1 - P(x <16.5)
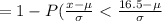
![= 1 - P{Z < [(16.5 - 14.94)/(3.67)]](https://img.qammunity.org/2020/formulas/computers-and-technology/college/xi1qwzpy7nsdm86j5nmycqr2fkzlahys4p.png)
= 1 - P{z< 0.425}
= 1 - 0.6628
P(x >16.5) = 0.3372