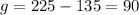Question

Last summer,at a camp,the ratio of the number of boy campers to girl campers is 9:6.If there is 225 campers,how many boy campers were there?How many girl campers?

Answer 1

Answer: There were 135 boy campers and 90 girl campers.

Explanation:

Let be "b" the number of boys campers and "g" the number of girl campers.

Given the following ratio of the number of boy campers to girl campers:

`9:6`

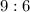
We know that for every 9 boys campers there were 6 girl camper; if we add them we get this sum:

`9+6=15\ campers`

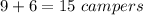
Knowing that there were a total of 225 campers, we can set up the following proportion in order to find the value of "b". Then, solving for "b" we get:

`(9)/(15)=(b)/(225)\\\\b=(225)((9)/(15))\\\\b=135`

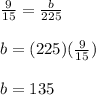
Finally, we get that the number of girl campers was:

`g=225-135=90`