Step-by-step explanation:
The equilibrium constant of the reaction =
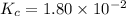
Initial concentration of HI = 0.311 M
After addition 0.174 mol of HI(g)
Concentration of HI added =

New concentration of HI = 0.311 M + 0.174 M = 0.485 M
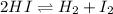
Initial concentration:
0.311 M
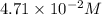
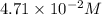
At equilibrium:
(0.485 M - x)


![K_(eq)=([H_2][I_2])/([HI]^2)](https://img.qammunity.org/2020/formulas/chemistry/college/jmdfl8r54o7ol5j8cv19awltl5fmdxaasr.png)
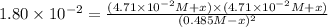
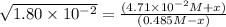

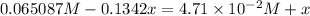
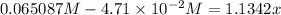
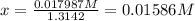
Equilibrium concentrations:
![[HI]=0.485 M-x = 0.485 M - 0.01586 M= 0.46914 M](https://img.qammunity.org/2020/formulas/chemistry/college/4j8ts113jz0neb0ywiuceb2a9006dfm7y8.png)
![[H_2]=[I_2]=4.71* 10^(-2) M+x=4.71* 10^(-2) M+0.01586 M](https://img.qammunity.org/2020/formulas/chemistry/college/zxavebe5csjdtsoe8wcfhl7jzsvr93qhbs.png)
![[H_2]=[I_2]=0.06296 M](https://img.qammunity.org/2020/formulas/chemistry/college/r5gx7xbxfa5hkbb3jmc5yk7clpharqbxne.png)