Question

Wells, Inc., has identified an investment project with the following cash flows. Year Cash Flow 1 $ 1,060 2 1,290 3 1,510 4 2,250 a. If the discount rate is 6 percent, what is the future value of these cash flows in Year 4? (Do not round intermediate calculations and round your answer to 2 decimal places, e.g., 32.16.) b. What is the future value at an interest rate of 14 percent? (Do not round intermediate calculations and round your answer to 2 decimal places, e.g., 32.16.) c. What is the future value at an interest rate of 21 percent?

Answer 1

The future value of the cash flows in Year 4 is calculated for discount rates of 6%, 14%, and 21%.

Step-by-step explanation:

To calculate the future value of cash flows, we need to use the formula:

`\[ FV = \sum_(t=1)^(n) \left( CF_t * (1 + r)^(n-t+1) \right) \]`

Where:

-
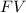`\(FV\)` = Future Value

-
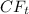`\(CF_t\)` = Cash flow at time \(t\)

-
`\(r\)` = Discount rate

-
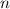`\(n\)` = Total number of periods or cash flows

Using this formula, we can calculate the future value of the cash flows in Year 4 for different discount rates:

1. At a discount rate of 6%, the future value is $2,787.50
2. At a discount rate of 14%, the future value is $3,542.99
3. At a discount rate of 21%, the future value is $4,298.88

Answer 2

Instructions are listed below

Step-by-step explanation:

Giving the following information:

Cash Flow:

1 $ 1,060

2 1,290

3 1,510

4 2,250

A) i= 0.06

FV= PV*(1+i)^n

1= 1060*(1.06)^4= $1,338.23

2= 1290*(1.06^3= $1,536.41

3= $1,696.64

4= $2,385

Total= $6,956.28

B) i=14%

1= 1060*(1.14^4)= $1,790.30

2= $1,911.19

3= $1,962.40

4= $2,565

Total= $8,28.90

C) i= 21%

FV= $9,490.81