Question

Using Gibbs Equation, dU=TdS-pdV show that (dS/dV) at a constant U =P/T. The reciprocal of (dS/dU)v = 1/T.

Answer 1

Step-by-step explanation:

dU=TdS-pdV (given)

To prove = 1)
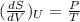`((dS)/(dV))_U=(P)/(T)` (at constant U)

2)
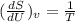`((dS)/(dU))_v=(1)/(T)` (at constant V)

Solution: 1)

dU=TdS-PdV

`PdV=TdS-dU`

`P=((TdS))/(dV)-(dU)/(dV)`

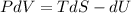
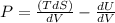
Derivative of constant is zero.

Given that internal energy is ,U = constant

`P=T(dS)/(dV)-0`

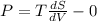
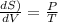`(dS))/(dV)=(P)/(T)` (hence proved)

Solution: 2)

dU=TdS-PdV

Differentiating with respect to dU, we get:

`((dU)/(dU))_v=T((dS)/(dU))_v-P((dV)/(dU))_v`

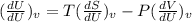
Derivative of constant is zero.

Given that volume is constant , V= constant

`1=T((dS)/(dU))_v`

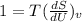
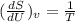`((dS)/(dU))_v=(1)/(T)` (hence proved)