Question

Applied linear algebraA manufacturer produces desks and bookcases. Desks d require 5 hours of cutting time and 10 hours of assembling time. Bookcases b require 15 minutes of cutting time and one hour of assembling time. Each day, the manufacturer has available 200 hours for cutting and 500 hours for assembling. The manufacturer wants to know how many desks and bookcases should be scheduled for completion each day to utilize all available work power. Show that this problem is equivelent to solving two equatinos in the two unknowns d and b.

Answer 1

30 desks

200 bookcases

Explanation:

Hello!

To solve this problem we must propose 2 linear equations as follows.

1.for the cutting time = if we multiply the number of desks (D) by the cutting time (5h) plus the number of bookcases (B) by the cutting time (15min = 0.25h), it will result in the Total available cutting time = 200h

1.For the time of the assembly = if we multiply the number of desks (D) by the time of assembly (10h) plus the number of bookcases (B) by the time of assembly (1h), it will result in the total time available of assembly = 500h.

taking into account the above we infer the following equations

5D+0.25B=200 (ecuation number 1)

10D+B=500 (ecuation number 2)

Now what we have to do is solve the system of two linear equations and two unknowns, for which we will take equation number 1 multiply it by four and subtract equation 2, then apply algebra

4(1)-(2)

20D+B=800

-

10D+B=500

---------------------------

10D=300

`D=(300)/(100) =30Desks`

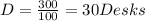
Now we use equation number 2 to find the number of book cases

10D+B=500

B=500-10D

B=500-10(30)=200bookcases

Answer 2

Explanation:

Let d= number of desks and b= number of bookcases.

Since each day the number of hours available for cutting is 200, then the amount of desks produced by the cutting time of one desk plus the amount of bookcases produced by the cutting time of one bookcase must be 200. This means that

5d+1/4b=200

Now, since each day the number of hours available for assembling time is 500, then the amount of desks produced by the assembling time of one desk plus the amount of bookcases produced by the assembling time of one bookcase must be 500. This means that

10d+b=500

Then, solve this problem is equivalent to solve the following linear system

`5d+(1)/(4)b=200 \\10d+b=500` in the two unknowns d and b