Answer:
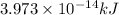 is the result in kiloJoules.
is the result in kiloJoules.
Step-by-step explanation:
Value of given Planck constant = h=
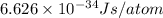
Energy emitted by 1 atom in a 1 sec :

2.00 min =
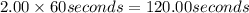
Energy emitted by 1 atom in 120 seconds = E'
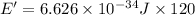
Let the energy emitted by
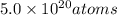 in 2.00 minutes be E.
in 2.00 minutes be E.
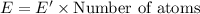
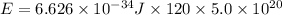
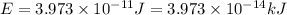
(1 J = 0.001 kJ)
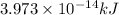 is the result in kiloJoules.
is the result in kiloJoules.