Question

Question 2 Calculate the pH of a solution that has an acetic acid concentration of 0.05 M and a sodium acetate concentration of 0.075 M. (a) By making use of the Henderson - Hasselbach equation. (b) Without making any assumptions. (4) (6) 1101

Answer 1

Answer : The pH of the solution is, 4.9

Explanation : Given,

Dissociation constant for acetic acid =
`K_a=1.8* 10^(-5)`

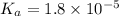
Concentration of acetic acid = 0.05 M

Concentration of sodium acetate = 0.075 M

First we have to calculate the value of
`pK_a`.

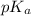The expression used for the calculation of
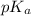`pK_a` is,

`pK_a=-\log (K_a)`

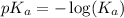
Now put the value of
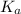`K_a` in this expression, we get:

`pK_a=-\log (1.8* 10^(-5))`

`pK_a=5-\log (1.8)`

`pK_a=4.7`

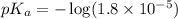
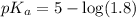
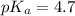
Now we have to calculate the pH of buffer.

Using Henderson Hesselbach equation :

`pH=pK_a+\log ([Salt])/([Acid])`

`pH=pK_a+\log ([CH_3COONa])/([CH_3COOH])`

Now put all the given values in this expression, we get:

`pH=4.7+\log ((0.075)/(0.05))`

`pH=4.9`

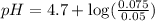
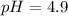
Therefore, the pH of the solution is 4.9.