Answer:
The velocity of the first person is 2.9795 m/s and the velocity of the second person is 0.0275 m/s
Step-by-step explanation:
First, we are going to study the interacción between the ball and the first person. In every case the linear momentum is conserved so:
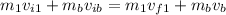
Where
 is the mass of the first person,
is the mass of the first person,
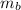 is the mass of the ball,
is the mass of the ball,
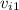 and
and
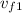 are the initial and final velocities of the first person,
are the initial and final velocities of the first person,
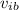 is the initial velocities of the ball and
is the initial velocities of the ball and
 is the velocity of the ball once it is throws.
is the velocity of the ball once it is throws.
So, if we replace the values and solve for
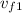 , we get:
, we get:
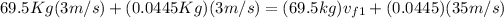
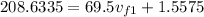
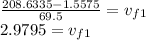
Therefore, the velocity of the first person after the snowball is exchanged is 2.9795 m/s
Now, we are going to study the interaction between the ball and the second person, we get:
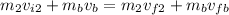
Where
 is the mass of the second person,
is the mass of the second person,
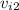 is the initial velocity of the second person,
is the initial velocity of the second person,
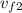 is the final velocity of the second person and
is the final velocity of the second person and
 is the final velocity of the ball.
is the final velocity of the ball.
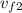 is equal to
is equal to
 , so if we replace the values and solve for
, so if we replace the values and solve for
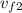 , we get:
, we get:
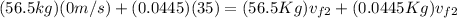

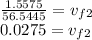
Finally, the the velocity of the second person after the snowball is exchanged is 0.0275 m/s