Answer:
The mean of Z, the total number of customers that enter these locations in an hour is 110.
Explanation:
Consider the provided information.
Let X be the number of customers that enter the center of town location in an hour,
Let Y be the number of customers that enter the location at the west end of town in an hour.
Assuming that
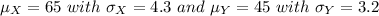
X and Y are independent random variables.
The expected value of the sum of random variables is equal to the sum of their individual expected values.

Hence, the mean of Z, the total number of customers that enter these locations in an hour is 110.