Question

The decomposition reaction: SO,Cl, SO2 + Cl2, has a first order rate constant of 2.2 x 10's at 320 °C. If the initial concentration of SO2Cl2 is 0.0040 M, what will be its concentration be (a) after 1.00 hr and (b) after 1.00 day?

Answer 1

(a) The concentration of
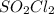`SO_2Cl_2` after 1.00 hr will be 0.0037 M

(b) The concentration of
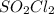`SO_2Cl_2` after 1.00 day will be 0.00060 M

Explanation :

(a) The expression for first order reaction is:

`[C_t]=[C_o]e^(-kt)`

where,

`[C_t]` = concentration of
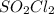`SO_2Cl_2` at time 't' = ?

`[C_o]` = concentration of
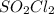`SO_2Cl_2` at time '0' = 0.0040 M

k = rate constant =
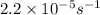`2.2* 10^(-5)s^(-1)` (assuming the power of 10 from the correct source)

t = time = 1.00 hr = 3600 s (1 hr = 3600 s)

Now put all the given values in the above expression, we get:

`[C_t]=(0.0040)* e^{-(2.2* 10^(-5))* (3600)}`

`[C_t]=0.0037M`

Thus, the concentration of
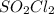`SO_2Cl_2` after 1.00 hr will be 0.0037 M

(b) The expression for first order reaction is:

`[C_t]=[C_o]e^(-kt)`

where,

`[C_t]` = concentration of
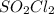`SO_2Cl_2` at time 't' = ?

`[C_o]` = concentration of
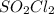`SO_2Cl_2` at time '0' = 0.0040 M

k = rate constant =
`2.2* 10^(-5)s^(-1)`

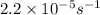
t = time = 1.00 day = 86400 s (1 day = 86400 s)

Now put all the given values in the above expression, we get:

`[C_t]=(0.0040)* e^{-(2.2* 10^(-5))* (86400)}`

`[C_t]=0.00060M`

Thus, the concentration of
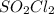`SO_2Cl_2` after 1.00 day will be 0.00060 M