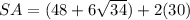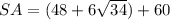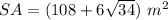Answer:
Part a) The lateral area of the prism is
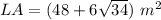
Part b) The surface area of the prism is
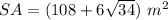
Explanation:
Part a) What is the lateral area of the prism?
we know that
The lateral area of the prism is
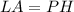
where
P is the perimeter of the base
H is the height of the prism
we have
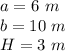
The perimeter of the base is
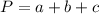
Find the hypotenuse of the right triangle
Applying the Pythagoras Theorem

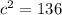

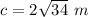
Find the perimeter of the base P
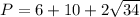

Find the lateral area of the prism
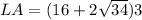
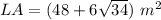
Part b) What is the total surface area?
The total surface area is
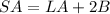
where
LA is the lateral area
B is the area of the base
Find the area of the base
Remember that the base is a triangle so
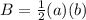
we have
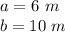
substitute


Find the surface area of the prism
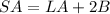
we have

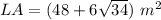
substitute