Answer:
The magnitude of the electric field and direction of electric field are
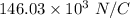 and 75.36°.
and 75.36°.
Step-by-step explanation:
Given that,
First charge

Second charge
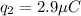
Distance between two corners r= 50 cm
We need to calculate the electric field due to other charges at one corner
For E₁
Using formula of electric field

Put the value into the formula
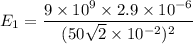
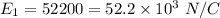
For E₂,
Using formula of electric field
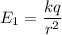
Put the value into the formula
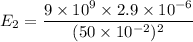
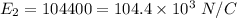
We need to calculate the horizontal electric field
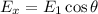
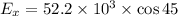
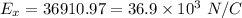
We need to calculate the vertical electric field
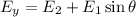
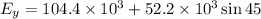

We need to calculate the net electric field
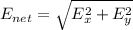
Put the value into the formula
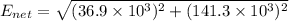
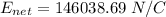
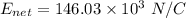
We need to calculate the direction of electric field
Using formula of direction
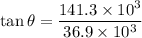
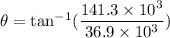
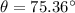
Hence, The magnitude of the electric field and direction of electric field are
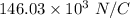 and 75.36°.
and 75.36°.