Question

The speed limit on a particular city street is 45 miles per hour (which is 20 m/s). A driver approaching a stoplight slam on their brakes, locking the wheels of their car in place so that they no longer rotate. Part A: If the coefficient of friction between the car's tires and the street is 0.85, what is the minimum distance the driver would need to start braking in order to stop before the intersection? Part B: When it rains, the coefficient of friction drops to 0.45. If the driver still wants to be able to stop in the same distance as in part A, what is the maximum speed they can have when it rains?

Answer 1

23.98 m

14.55058 m/s

Step-by-step explanation:

t = Time taken

u = Initial velocity

v = Final velocity

s = Displacement

g = Acceleration due to gravity = 9.81 m/s²

`v^2-u^2=2g\mu s\\\Rightarrow s=(v^2-u^2)/(2g\mu)\\\Rightarrow s=(0^2-20^2)/(2* 9.81* -0.85)\\\Rightarrow s=23.98\ m`

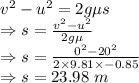
Minimum distance the driver would need to start braking in order to stop before the intersection is 23.98 m

`v^2-u^2=2\mu gs\\\Rightarrow -u^2=2\mu gs-v^2\\\Rightarrow u=√(v^2-2\mu gs)\\\Rightarrow u=√(0^2-2* 9.81* -0.45* 23.98)\\\Rightarrow u=14.55058\ m/s`

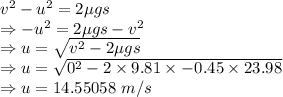
The speed would be 14.55058 m/s