Question

Kevin walks 50.0 m to the east and 30.0 m at 30 degrees north of east. a) Sketch Kevin's move. b) What is the magnitude and direction of Kevin's overall displacement?

Answer 1

a) see attached figure.

b) The magnitude of Kevin´s overall displacement is 77.5 m.

The direction of the overall displacement is 11.2° north of east.

Step-by-step explanation:

Please, see the attached figure for a better understanding of the problem.

The resultant overall displacement will be the sum of the vectors A+B (see figure).

The vector A is horizontal, it has no vertical component. Then:

A = (50.0 m, 0)

The vector B, in change, has a vertical and horizontal component. Applying trigonometry of right triangles we can find the components of B:

By trigonometry:

cos θ = adjacent / hypotenuse

sin θ = opposite / hypotenuse

In this case:

cos 30° = x-component of B / magnitude of B

cos 30° = x-B / 30.0 m

30.0 m · cos 30° = x-B

x-B = 26.0 m

sin 30° = y-component of B / 30.0 m

30.0 m · sin 30° = y-B

y-B = 15.0 m

Then, the vector B will be:

B = (26.0 m, 15.0m)

The overall displacement will be:

R = A + B

R = (50.0 m, 0) + (26.0 m, 15.0 m)

R = (50.0 m + 26.0, 0 + 15.0 m)

R = (76 m, 15 m)

The magnitude of the overall displacement will be:

`|R| = \sqrt{(76 m)^(2) + (15 m)^(2)} = 77.5 m`

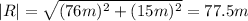
The magnitude will be 77.5 m.

Using trigonometry, we can find its direction (see figure):

cos θ = 76 m / magnitude of R

θ = 11.2°

The direction of the overall displacement is 11.2° north of east.